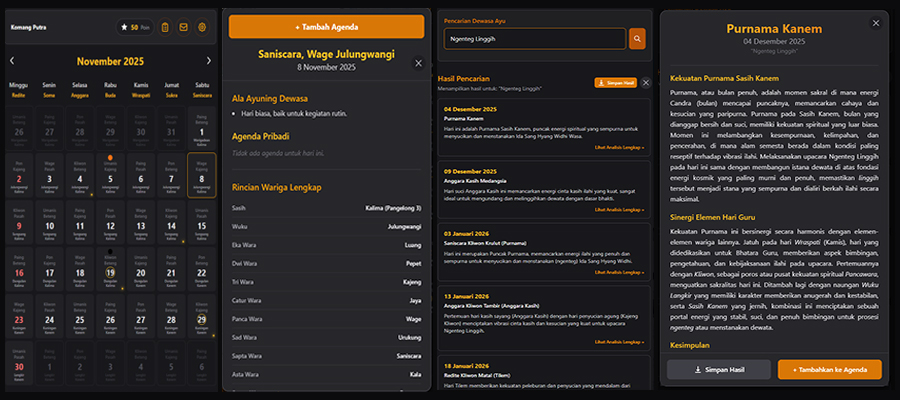
Algoritma Rumus Pengalantaka Purnama – Tilem

Sistem penanggalan Bali, atau yang lebih dikenal sebagai Kalender Saka Bali, bukanlah sekadar alat penunjuk waktu, melainkan sebuah instrumen matematis yang kompleks untuk menyelaraskan ritme mikrokosmos (kehidupan manusia) dengan makrokosmos (pergerakan benda langit). Berbeda dengan kalender Gregorian yang murni berbasis matahari (solar) atau kalender Hijriah yang murni berbasis bulan (lunar), Kalender Saka Bali mengadopsi sistem hibrida lunisolar yang diperkaya dengan siklus aritmatika lokal yang disebut Pawukuan. Kompleksitas ini menuntut adanya sistem perhitungan yang presisi untuk menentukan titik-titik sakral waktu, terutama Purnama (bulan penuh) dan Tilem (bulan mati).

Pertanyaan mengenai “rumus” perhitungan Purnama dan Tilem sesungguhnya mengarah pada jantung dari sistem astronomi tradisional Bali yang disebut Wariga. Di dalam Wariga, terdapat sebuah mekanisme koreksi waktu yang disebut Pengalantaka. Pengalantaka adalah algoritma “warisan leluhur” yang berfungsi sebagai jembatan matematis antara siklus Wuku (210 hari) dengan siklus bulan sinodis (29,53 hari).1 Tanpa adanya Pengalantaka, kalender Bali akan mengalami desinkronisasi fatal antara “hari ritual” dan “fenomena langit” yang sebenarnya, yang dalam teologi Hindu-Bali dapat membatalkan keabsahan sebuah upacara Yadnya.

Laporan penelitian ini menyajikan analisis komprehensif mengenai mekanisme perhitungan tersebut. Kami akan membedah anatomi waktu Bali, menurunkan rumus-rumus matematis yang mendasarinya, menganalisis pergeseran sekuler “Eka Sungsang” yang memprediksi perubahan algoritma hingga abad ke-24, dan menyusun logika komputasi bagi implementasi modern. Analisis ini didasarkan pada data tekstual lontar, studi astronomi modern, dan algoritma perangkat lunak kalender yang ada.

Landasan Astronomis dan Struktur Kalender Saka

Sebelum melangkah pada derivasi rumus, sangat krusial untuk memahami tiga lapisan waktu yang berjalan paralel dalam sistem kalender Bali. Ketiga lapisan ini bergerak dengan kecepatan berbeda namun harus bertemu pada satu titik koordinat waktu yang presisi.

Tiga Poros Waktu (Tri-Pramana)

Sistem kalender Bali dibangun di atas integrasi tiga siklus utama:

1. Tahun Surya (Solar Year) : Berbasis pada revolusi Bumi mengelilingi Matahari. Durasi rata-ratanya adalah 365,25 hari. Dalam tradisi Bali, ini tercermin dalam perhitungan Sasih (bulan) yang idealnya terikat pada musim, meskipun dalam praktiknya sering kali bergeser. Tahun Saka dimulai pada tahun 78 Masehi, yang dikenal sebagai era Saliwahana.
2. Tahun Candra (Lunar Year) : Berbasis pada revolusi Bulan mengelilingi Bumi. Satu siklus sinodis (dari bulan mati ke bulan mati berikutnya) rata-rata berdurasi 29,53059 hari. Satu tahun candra (12 bulan) berdurasi sekitar 354 hari. Selisih ~11 hari dengan tahun surya inilah yang menuntut adanya bulan kabisat atau Mala Sasih.
3. Tahun Wuku (Pawukuan) : Sebuah siklus aritmatika murni yang khas Nusantara, terdiri dari 30 minggu (Wuku) dimana setiap minggu terdiri dari 7 hari. Total siklus adalah 30×7=21030 \times 7 = 21030×7=210 hari. Siklus ini tidak memiliki korelasi astronomis langsung dengan benda langit, namun berfungsi sebagai “kendaraan” atau kerangka acuan bagi penanggalan lunar.

Anomali Lunar dan Konsep Tithi

Inti permasalahan dalam menghitung Purnama dan Tilem adalah definisi “hari”. Dalam kalender Masehi, hari didefinisikan oleh Matahari (terbit ke terbit). Dalam astronomi Hindu-Bali, hari lunar disebut Tithi.

Satu Tithi didefinisikan bukan oleh waktu, melainkan oleh jarak sudut (elongasi) antara Matahari dan Bulan.

• Lingkaran penuh ekliptika adalah 360∘360^{\circ}360∘.
• Dibagi menjadi 30 Tithi (15 Tithi Shukla Paksha/terang dan 15 Tithi Krishna Paksha/gelap).
• Maka, 1 Tithi = 12∘12^{\circ}12∘ pergerakan relatif Bulan terhadap Matahari.

Karena Bulan bergerak lebih cepat (~13∘13^{\circ}13∘ per hari) dibandingkan Matahari (~1∘1^{\circ}1∘ per hari), jarak sudut 12∘12^{\circ}12∘ tersebut ditempuh dalam waktu kurang dari satu hari surya, tepatnya sekitar 0,9843 hari surya.

• Implikasi Matematis: Dalam kurun waktu 63 hari surya, Bulan akan menyelesaikan sekitar 64 Tithi.
• Konsekuensi: Ada satu Tithi yang harus “dibuang” atau dilewati dalam penamaan hari kalender setiap ~63 hari agar perhitungan tetap sinkron dengan Matahari. Fenomena ini disebut Ngunaratri (pengurangan hari).

Rumus perhitungan Purnama dan Tilem pada dasarnya adalah algoritma untuk memprediksi kapan tepatnya Ngunaratri ini terjadi. Sistem yang mengatur prediksi ini adalah Pengalantaka.

Algoritma Pengalantaka : Jantung Perhitungan Wariga

Berdasarkan literatur lontar dan kajian akademis, Pengalantaka didefinisikan sebagai tabel koreksi atau pedoman aritmatika untuk menetapkan umur bulan (apakah 29 atau 30 hari) dan letak Purnama-Tilem.

Siklus 63 Hari (9 Wuku)

Unit waktu dasar dalam Pengalantaka bukanlah tahun atau bulan, melainkan siklus 63 hari. Angka ini didapat dari kelipatan persekutuan terkecil yang mendekati sinkronisasi antara hari surya dan hari lunar.

Mengapa 63 hari?

• 9 Wuku ×\times× 7 hari = 63 hari.
• Dalam 63 hari surya, terjadi akumulasi selisih waktu lunar yang mendekati 1 hari penuh (karena 1 lunasi = 29,53 hari, dua lunasi = 59,06 hari. Sisa hari dan pecahan tithi terakumulasi).
• Sistem Bali menetapkan bahwa penyesuaian (pemotongan hari) dilakukan setiap periode 9 Wuku ini.

Struktur Penanggal dan Panglong

Satu bulan kalender Bali (Sasih) dibagi menjadi dua paruh:

1. Penanggal (Shukla Paksha) : Periode dari Tilem menuju Purnama (Bulan membesar). Hari pertamanya disebut Penanggal 1 (sehari setelah Tilem).
2. Panglong (Krishna Paksha) : Periode dari Purnama menuju Tilem (Bulan mengecil). Hari pertamanya disebut Panglong 1 (sehari setelah Purnama).

Idealnya, Penanggal terdiri dari 15 hari dan Panglong terdiri dari 15 hari (15+15=3015+15=3015+15=30). Namun, karena rata-rata bulan sinodis hanya 29,53 hari, maka tidak mungkin setiap bulan berumur 30 hari. Harus ada bulan-bulan yang berumur 29 hari.

• Rumus Dasar (Urfi/Pendekatan) : Bulan ganjil berumur 30 hari, bulan genap berumur 29 hari.
• Rumus Pengalantaka (Haqiqi/Presisi) : Koreksi dilakukan bukan sekadar ganjil-genap, tapi berdasarkan jatuhnya siklus 9 Wuku. Pengurangan hari bisa terjadi pada paruh Penanggal (menjadi 14 hari) atau paruh Panglong (menjadi 14 hari).

Mekanisme “Sungsang-Pahing” (The Anchor Point)

Sistem Pengalantaka bekerja seperti roda gigi yang berputar di atas roda gigi Wuku. Titik temu antara roda gigi ini bergeser seiring waktu. Titik temu atau “jangkar” perhitungan ini dinamakan berdasarkan nama Wuku dan nama Pancawara (hari pasaran 5-harian).

Data dari memberikan wawasan yang sangat mendalam dan teknis mengenai pergeseran titik jangkar ini, yang disebut Eka Sungsang. Ini adalah parameter paling vital dalam rumus perhitungan:

Periode Waktu (Masehi)	Konfigurasi Pengalantaka (Rumus Dasar)	Puncak Akurasi
Abad 20 s.d. 2117	Eka Sungsang ka Pahing	2050
2117 s.d. 2236	Eka Sungsang ka (Soma) Umanis	2175
2236 s.d. 2361	Eka Sungsang ka Radite Kliwon	2300
2361 s.d. Masa Depan	Eka Juluwangi ka Saniscara Wage	2420

Analisis Implikasi:

Rumus perhitungan untuk tahun 2024 atau 2025 wajib menggunakan parameter Eka Sungsang ka Pahing. Artinya, siklus koreksi 63 hari dihitung mulai dari pertemuan antara Wuku Sungsang (Wuku ke-10) dengan hari Pahing. Jika seorang penyusun kalender menggunakan rumus lama atau rumus masa depan, perhitungan Purnama/Tilem akan meleset 1 hari dari posisi bulan yang sebenarnya.

Pergantian parameter ini dijadwalkan secara spesifik. Misalnya, pada tanggal 9 November 2117, sistem harus “reset” dan beralih ke parameter Sungsang ka Umanis. Hal ini menunjukkan bahwa leluhur Bali telah memprediksi presesi equinox dan akumulasi error ribuan tahun ke depan.

Derivasi Rumus Perhitungan

Berdasarkan sintesis dari snippet 3, berikut adalah derivasi rumus operasional untuk menghitung Purnama dan Tilem. Rumus ini dapat diadopsi baik untuk perhitungan manual maupun algoritma perangkat lunak.

Untuk menghitung tanggal Purnama/Tilem pada tahun Saka tertentu (YsY_sYs​):

1. Tahun Saka (YsY_sYs​): Contoh, tahun 2025 Masehi = Saka 1947 (2025 – 78).
2. Wuku Jangkar (PanchorP_{anchor}Panchor​): Untuk era sekarang, nilainya adalah Wuku Sungsang (Index 10).
3. Pancawara Jangkar (DanchorD_{anchor}Danchor​): Untuk era sekarang, nilainya adalah Pahing (Index 2 dalam siklus 5 hari: Umanis, Pahing, Pon, Wage, Kliwon).
4. Daftar Wuku (WlistW_{list}Wlist​): Urutan 1-30 (Sinta s.d. Watugunung).

Langkah 1 : Menentukan Posisi Wuku Harian

Setiap hari dalam kalender Bali memiliki koordinat (W,S,P)(W, S, P)(W,S,P) dimana WWW=Wuku, SSS=Saptawara (Minggu-Sabtu), PPP=Pancawara.

Rumus mencari Wuku hari ini dari Julian Day number (JDJDJD):

Langkah 2 : Logika Siklus 9 Wuku (Pengalantaka)

Sistem Pengalantaka membagi waktu menjadi blok-blok 63 hari. Titik awal blok ini ditandai oleh pertemuan Wuku-Wuku spesifik.

Mengutip 7, Wuku-wuku pemicu koreksi (adjustment triggers) adalah:

1. Sungsang (Wuku 10)
2. Tambir (Wuku 19)
3. Kulawu (Wuku 28)
4. Wariga (Wuku 7)
5. Pahang (Wuku 16)
6. Bala (Wuku 25)

Perhatikan pola matematika di sini: Jarak antar wuku tersebut adalah persis 9 minggu.

Setiap kali kalender melewati salah satu Wuku di atas (pada hari yang bersesuaian dengan Pancawara Pahing, sesuai aturan Eka Sungsang ka Pahing), maka sistem algoritma harus mengecek akumulasi umur bulan.

Rumus Logika Koreksi :

Jika hari ini berada dalam siklus Wuku Pemicu, maka :

• Cek sisa umur bulan (Moon Age).
• Jika umur bulan aritmatika menuntut 30 hari, namun Pengalantaka memberi sinyal “Ngunaratri” (pengurangan), maka umur bulan dipangkas menjadi 29 hari.
• Pengurangan ini biasanya dilakukan dengan memendekkan Penanggal menjadi 14 hari (Purnama jatuh sehari lebih cepat) atau Panglong menjadi 14 hari (Tilem jatuh sehari lebih cepat).

Langkah 3 : Perhitungan Posisi Bulan (Tithi) Modern

Untuk verifikasi akurasi (seperti pada aplikasi modern 4), rumus aritmatika tradisional di atas disandingkan dengan Hisab Haqiqi (perhitungan astronomis murni).

Algoritma Jean Meeus untuk Tithi :

1. Hitung Bujur Ekliptika Matahari (λsun\lambda_{sun}λsun​) dan Bulan (λmoon\lambda_{moon}λmoon​) pada jam 06:00 WITA (Matahari terbit di Bali).
2. Hitung Elongasi (DDD):

   D=λmoon−λsunD=λmoon−λsunD=λmoon​−λsun​ D=λmoon−λsunD = \lambda_{moon} – \lambda_{sun}D=λmoon​−λsun​ D=λmoon−λsunD=λmoon​−λsun​D=λmoon​−λsun​

   (JikaD<0D<0D<0,tambahkan360∘360∘360∘) (Jika D<0D < 0D<0, tambahkan 360∘360^{\circ}360∘) (JikaD<0D<0D<0,tambahkan360∘360∘360∘)

3. Hitung Tithi Index (TTT):

   T=⌊D12⌋+1T=⌊D12⌋+1T=⌊12D​⌋+1 T=⌊D12⌋+1T = \lfloor \frac{D}{12} \rfloor + 1T=⌊12D​⌋+1 T=⌊D12⌋+1T=⌊12D​⌋+1T=⌊12D​⌋+1

4. Penentuan Purnama: Jika T=15T=15T=15 T=15T = 15T=15 T=15T=15T=15 pada saat matahari terbit, hari tersebut adalah Purnama. Namun, jika elongasi mencapai 180∘180∘180∘ 180∘180^{\circ}180∘ 180∘180∘180∘ (puncak Purnama) setelah terbit matahari dan sebelum terbit besok, aturan Tithi menjadi kompleks (tergantung Dewa Yasa atau aturan toleransi).
5. Penentuan Tilem: Jika T=30T=30T=30 T=30T = 30T=30 T=30T=30T=30 (atau 0) pada saat matahari terbit, hari tersebut adalah Tilem.

Aplikasi Kalender Bali berbasis Android 4 menggunakan pendekatan hibrida ini: menggunakan algoritma astronomis untuk mendapatkan posisi benda langit, lalu memetakannya ke dalam grid Wuku dan Sasih tradisional untuk penamaan.

Dinamika Mala Sasih : Algoritma Bulan Kabisat

Laporan ini tidak akan lengkap tanpa membahas penanganan Mala Sasih (Bulan Kabisat), karena Purnama dan Tilem bergantung pada bulan apa yang sedang berjalan. Ketidaksesuaian antara 12 bulan lunar (354 hari) dan tahun surya (365 hari) menyebabkan kalender lunar “maju” sekitar 11 hari per tahun.

Aturan Metonik Bali

Dalam siklus 19 tahun surya (Siklus Meton), terdapat 235 bulan lunar. Agar kalender tetap Lunisolar (Sasih Kadasa tetap jatuh sekitar Maret/April dan tidak bergeser ke Januari seperti Ramadan), harus disisipkan 7 bulan tambahan dalam periode 19 tahun tersebut.

Rumus Penentuan Nampih Sasih

Berdasarkan tradisi Wariga yang tercatat dalam manuskrip dan diterapkan dalam sistem, bulan sisipan (Nampih Sasih) terjadi ketika dalam satu bulan surya terdapat dua kali kejadian Tilem (Bulan Baru).

• Logika : Bulan Surya rata-rata 30-31 hari. Bulan Lunar 29.5 hari. Sangat mungkin satu bulan lunar “tertelan” utuh di dalam satu bulan surya.
• Jika ini terjadi, bulan tersebut dianggap “Mala” (kotor/ganda). Bulan pertama disebut Mala Sasih (misal: Mala Jiyestha), bulan kedua disebut Sasih Nampih atau bulan utamanya (Jiyestha).
• Implikasi pada Purnama: Pada tahun dengan Mala Sasih (tahun dengan 13 bulan), akan terdapat 13 kali Purnama dan 13 kali Tilem. Perhitungan rumus harus mampu mendeteksi keberadaan bulan ke-13 ini agar urutan Sasih berikutnya (Kasa, Karo, dst.) tidak kacau.

Implementasi Teknis dan Tantangan Digitalisasi

Dalam era digital, seperti yang ditunjukkan oleh snippet, perhitungan ini ditransformasikan menjadi kode pemrograman. Tantangan utama yang dihadapi pengembang adalah mereplikasi logika “fleksibel” dari pedanda/ahli wariga ke dalam logika “biner” komputer.

Tabel Konversi Data untuk Pengembang

Berikut adalah tabel referensi data yang diperlukan untuk membangun rumus komputasi kalender Bali, mensintesis data dari 5:

Komponen	Nilai / Aturan	Keterangan
Epoch Saka	Tahun Masehi – 78	Awal Tahun Saka biasanya Nyepi (Maret/April)
Durasi Lunasi	29.53059 hari	Konstanta astronomi
Pola Sasih (Urfi)	Ganjil=30, Genap=29	Pola dasar sebelum koreksi Pengalantaka
Trigger Pengalantaka	Setiap 63 hari	Wuku Sungsang, Tambir, Kulawu, Wariga, Pahang, Bala
Tahun Eka Sungsang	Pahing (Hingga 2117)	Parameter kunci untuk abad ke-21
Ambang Batas Purnama	Elongasi 168∘−180∘168∘−180∘168∘−180∘ 168∘−180∘168^{\circ} – 180^{\circ}168∘−180∘ 168∘−180∘168∘−180∘168∘−180∘	Tithi ke-15 (Purnama)
Ambang Batas Tilem	Elongasi 348∘−360∘348∘−360∘348∘−360∘ 348∘−360∘348^{\circ} – 360^{\circ}348∘−360∘ 348∘−360∘348∘−360∘348∘−360∘	Tithi ke-30 (Tilem)

Pseudo code Logika Penentuan

Sebuah fungsi sederhana untuk menentukan apakah suatu hari adalah Purnama berdasarkan rumus Wariga (pendekatan):

FUNCTION IsPurnama(TanggalInput):

1. Hitung SelisihHari dari Epoch (Misal: 1 Saka 1940)
2. Hitung PosisiWuku = (SelisihHari DIV 7) MOD 30
3. Hitung PosisiPancawara = SelisihHari MOD 5
4. Cek Pengalantaka: IF PosisiWuku IN AND PosisiPancawara == Pahing: Set CorrectionFlag = TRUE (Ngunaratri aktif)
5. Hitung PerkiraanTithi: Tithi = (SelisihHari * 0.9843) MOD 30
6. Terapkan Koreksi: IF CorrectionFlag == TRUE: Tithi = Tithi + (FaktorKoreksi)
7. Evaluasi: IF Tithi >= 14.0 AND Tithi < 15.0: RETURN TRUE (Purnama) ELSE: RETURN FALSE

Catatan: Pseudocode ini adalah penyederhanaan. Implementasi nyata membutuhkan perhitungan floating-point presisi tinggi untuk posisi bulan.

Salah satu wawasan (insight) terpenting dari riset ini adalah sifat dinamis dari rumus itu sendiri. Tidak ada satu “Rumus Abadi”. Seperti yang dijelaskan dalam snippet 7, terdapat jadwal penggantian parameter Eka Sungsang.

Mengapa parameter harus diganti pada tanggal 9 November 2117?

Ini adalah bukti kecanggihan astronomi Bali kuno dalam memahami Presesi Ekuinoks.

• Sistem 63 hari adalah pendekatan aritmatika.
• Error yang dihasilkan sangat kecil (dalam orde menit per siklus), namun terakumulasi selama berabad-abad.
• Pada tahun 2117, akumulasi error tersebut akan mencapai 1 hari penuh.
• Jika sistem tidak diubah dari Sungsang ka Pahing menjadi Sungsang ka Umanis, maka Purnama yang tertera di kalender akan meleset 1 hari dari Purnama di langit.
• Pergeseran dari Pahing (urutan ke-2) ke Umanis (urutan ke-1) dan seterusnya menunjukkan pola mundur (retrograde), yang konsisten dengan fenomena presesi (mundurnya titik Aries).

Ini menunjukkan bahwa rumus perhitungan Purnama Tilem kalender Bali bukanlah dogma statis, melainkan algoritma adaptif yang memiliki mekanisme self-correction jangka panjang.

Implikasi Sosial dan Ritual

Ketepatan perhitungan rumus ini memiliki konsekuensi berat dalam struktur sosial masyarakat Bali.

• Validitas Yadnya: Upacara besar seperti Piodalan di Pura Besakih atau Tawur Agung bergantung mutlak pada ketepatan penentuan Purnama dan Tilem. Kesalahan hitung dianggap dapat mengundang bencana (ketidakharmonisan alam).
• Perdebatan Wariga vs. Astronomi: Sering terjadi perbedaan tanggal Purnama antara kalender yang diterbitkan oleh pengamat tradisional (menggunakan rumus aritmatika murni/Urfi) dengan kalender yang diterbitkan oleh institusi modern (menggunakan astronomi/Hisab Haqiqi). Dalam kasus ini, lembaga otoritatif seperti PHDI (Parisada Hindu Dharma Indonesia) biasanya melakukan Paruman (rapat dewan) untuk menetapkan tanggal resmi yang berlaku, seringkali memadukan kedua pendekatan: menggunakan astronomi untuk data posisi, namun menggunakan aturan Wariga untuk penamaan hari.

Perhitungan Purnama dan Tilem dalam Kalender Bali adalah sebuah sistem komputasi yang elegan dan rumit. Ia tidak dapat diringkas dalam satu persamaan linier sederhana y=mx+cy = mx + cy=mx+c, melainkan merupakan sistem algoritma bertingkat yang melibatkan:

1. Basis Wuku: Siklus 210 hari sebagai kerangka dasar.
2. Modul Pengalantaka: Siklus koreksi 63 hari (9 Wuku) untuk menyinkronkan hari surya dengan hari lunar.
3. Parameter Eka Sungsang: Variabel jangkar yang berubah setiap beberapa abad (saat ini: Sungsang-Pahing) untuk mengoreksi presesi sekuler.
4. Aturan Nampih: Logika penyisipan bulan ke-13 untuk menjaga keselarasan musim.

Bagi siapa pun yang hendak melakukan kalkulasi—baik secara manual maupun digital—ketaatan pada parameter Eka Sungsang ka Pahing (untuk abad ini) dan pemahaman akan mekanisme Ngunaratri pada titik-titik wuku pemicu (Sungsang, Tambir, dll) adalah syarat mutlak untuk mendapatkan hasil yang akurat dan sesuai dengan dresta (aturan baku) kalender Bali.